Sostituzione all'indietro

Nel caso della soluzione di un sistema lineare, il metodo di eliminazione di Gauss ci lascia con un sistema $U{\bf x}={\bf c}$ equivalente a quello originale. Essendo U triangolare, quest'ultimo sistema si risolve col metodo della back substitution. Vedi pagina 141 del libro di testo.

In forma matriciale, la sostituzione equivale a scrivere $U=D+\tilde{U}$, dove D è diagonale e $\tilde{U}$è strettamente triangolare. Quindi abbiamo

$$\begin{eqnarray*}(D+\tilde{U}){\bf x}&=& {\bf c} \\ D {\bf x}&=& {\bf c}- \tilde{U}{\bf x} \\ {\bf x}&=& D^{-1}({\bf c}-\tilde{U}{\bf x}) \end{eqnarray*}$$

Quest'ultima forma può sembrare irrisolubile perché ${\bf x}$ compare sia a sinistra che a destra. Si osservi invece che ogni elemento x_i a sinistra dipende solo dagli x_j con j>i. È dunque possibile calcolare i valori di x_i procedendo a ritroso, per $i=n,\ldots,1$:

$$x_i = {1 \over u_{ii}} \left( c_i - \sum_{j=i+1}^n u_{ij}x_j\right) \hspace{2cm} i=n,\ldots,1.$$

L'implementazione di questo procedimento è immediata. Supponendo di lavorare sempre sulla matrice a[][] e sul vettore b[], trasformati dal metodo di Gauss, abbiamo:

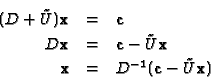
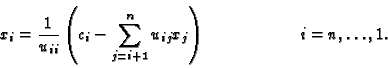
        for (i=n-1; i>=0; i--) {
            sum = 0.0;
            for (j=i+1; j<n: j++)
                sum = sum + a[i][j]*b[j];
            b[i] = ( b[i] - sum ) / a[i][i];
        }