Fattorizzazione LL^T

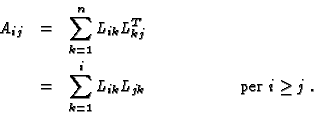
La fattorizzazione di una matrice simmetrica definita positiva A nella forma LL^T, con L triangolare inferiore, è associata al metodo di Cholesky. Per ottenere un algoritmo che calcoli la matrice L basta scrivere elemento per elemento la relazione A=LL^T:

$$\begin{eqnarray*}A_{ij} &=& \sum_{k=1}^n L_{ik}L^T_{kj} \\ &=& \sum_{k=1}^i L_{ik}L_{jk} \hspace{2cm}\mbox{per $i\geq j$ }. \end{eqnarray*}$$

Per j=i otteniamo

$$A_{jj} = \sum_{k=1}^j L_{jk}^2$$

da cui, togliendo il termine L_jj dalla sommatoria,

$$L_{jj} = \sqrt{ A_{jj} - \sum_{k=1}^{j-1} L_{jk}^2 }$$

che è la formula per gli elementi diagonali di L. Per gli altri abbiamo, analogamente,

$$L_{ij} = {1\over L_{jj}} \left( A_{ij}-\sum_{k=1}^{j-1}L_{ik}L_{jk} \right).$$

Queste formule sono dipendenti tra di loro, tuttavia calcolandole nell'ordine $j=1,\ldots,n$ e (fissato j) per $i=j+1,\ldots,n$, tutti i valori sono pronti quando servono. L'implementazione in C è immediata.

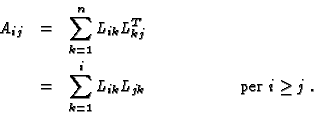
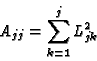
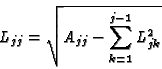
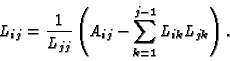
   for (j=0; j<n; j++) {
       for (sum=k=0; k<j; k++) sum += l[j][k]*l[j][k];
       l[j][j] = sqrt( a[j][j]-sum );
       for (i=j+1; i<n; i++) {
           for (sum=k=0; k<j; k++) sum += l[i][k]*l[j][k];
           l[i][j] = (a[i][j] - sum)/l[j][j];
       }
   }

Tramite la fattorizzazione LL^T è si possono risolvere sistemi lineari molto più velocemente che col metodo di Gauss (perché si riesce a sfruttare il fatto che A è definita positiva). Il sistema $A{\bf x}={\bf b}$ si trasforma in $LL^T{\bf x}={\bf b}$, che viene risolto risolvendo successivamente $L{\bf y}={\bf b}$ e $L^T{\bf x}={\bf y}$. Si tratta di due sistemi con matrice triangolare: il primo si risolve con una forward substitution:

   for (i=0; i<n; i++) {
       sum = 0.;
       for (j=0; j<i; j++) sum += l[i][j]*y[j];
       y[i] = (b[i] - sum) / l[i][i];
   }

ed il secondo con un'analoga backsubstitution:

   for (i=n-1; i>=0; i--) {
       sum = 0.;
       for (j=i+1; j<n; j++) sum += l[j][i]*x[j];
       x[i] = (y[i] - sum) / l[i][i];
   }

Se la matrice A non è definita positiva, il processo di fattorizzazione si blocca perché trova un radicando negativo. Nella pratica, questo è un buon modo per testare se una matrice data è definita positiva (un altro modo sarebbe calcolare gli autovalori, ma è molto più dispendioso!).

Una implementazione del metodo di Cholesky per la fattorizzazione LL^T e la risoluzione di sistemi lineari si trova in llt.c.